Salut tout le monde,
Aujourd'hui, nous allons discuter de la manière de calculer le périmètre d'un cercle et de la trigonométrie en général. Mais, avant cela, parlons de cette belle image ci-dessus, où nous voyons un cercle magnifique et parfait.
Le cercle
Le cercle est l'une des formes géométriques les plus simples. C'est essentiellement une ligne courbe qui se referme sur elle-même et qui a toujours la même distance entre tous les points de cette courbe, appelée le rayon. Le diamètre d'un cercle, quant à lui, est la distance qui sépare deux points diamétralement opposés de la courbe du cercle.
Cette image nous montre un cercle parfait, où nous pouvons clairement voir son rayon et son diamètre. Mais, comment pouvons-nous calculer le périmètre de ce cercle ?
Le périmètre d'un cercle
Le périmètre d'un cercle est la longueur de la courbe qui forme le cercle. Pour calculer le périmètre d'un cercle, nous avons besoin de connaître la valeur de son rayon ou de son diamètre.
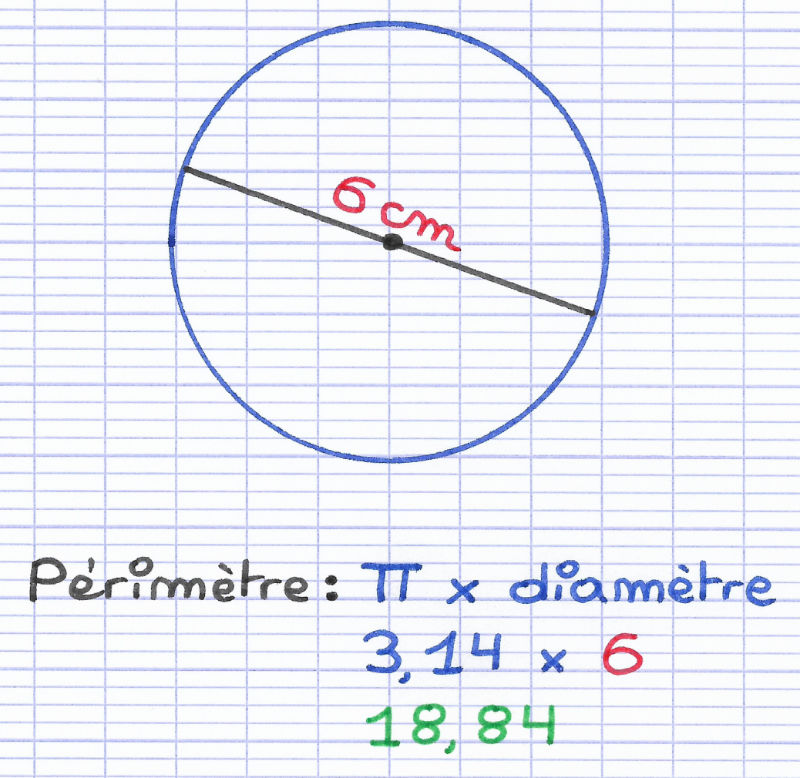
La formule pour calculer le périmètre d'un cercle est :
Périmètre = π × Diamètre
Ou bien :
Périmètre = 2 × π × Rayon
où π (pi) est une constante mathématique qui représente le ratio de la circonférence d'un cercle à son diamètre, et qui est d'environ 3,14.
Ainsi, pour calculer le périmètre du cercle dans notre image, nous avons besoin de la valeur de son diamètre, qui est clairement indiqué sur l'image. En appliquant la formule, nous obtenons :
P = π × 8 cm
ou bien :
P = 2 × π × 4 cm
ce qui donne un périmètre d'environ :
P ≈ 25,12 cm
Et voilà ! C'est aussi simple que ça ! Maintenant, parlons un peu de la trigonométrie, une branche des mathématiques qui se concentre sur les relations entre les angles et les côtés des triangles.
La trigonométrie
La trigonométrie est une discipline mathématique qui étudie les relations entre les angles et les côtés des triangles. Elle est utilisée dans divers domaines, tels que la science, l'ingénierie, l'architecture, la navigation, l'aviation, etc.
Les fonctions trigonométriques de base sont le sinus, le cosinus et la tangente, qui sont définies en fonction de l'angle d'un triangle et du rapport entre deux de ses côtés.
La trigonométrie est une branche complexe des mathématiques, qui nécessite beaucoup de pratique et de dévouement pour la maîtriser. Cependant, ses applications sont innombrables et elle peut être utile dans de nombreuses situations de la vie réelle.
C'est tout pour aujourd'hui ! J'espère que vous avez appris quelque chose de nouveau sur le cercle et la trigonométrie. N'hésitez pas à partager vos commentaires et vos questions dans la section des commentaires ci-dessous.
If you are looking for 3. Faire des cercles you've came to the right web. We have 6 Images about 3. Faire des cercles like Пин от пользователя Taha Kabiri на доске math | Тригонометрия, Физика и, feuille de formules sur les polygones et les cercles and also feuille de formules sur les polygones et les cercles. Here you go:
3. Faire Des Cercles
tecfa.unige.ch cercles formules visu tecfa xslt unige
Пин от пользователя Taha Kabiri на доске Math | Тригонометрия, Физика и
www.pinterest.com cercle trigonométrie formules cosinus et le les la pi maths cos sin sinus tangente tan calcul math circle choose board
Feuille De Formules Sur Les Polygones Et Les Cercles
studylibfr.com cercles formules polygones feuille
Calculer Le Périmètre D'un Cercle
math-coaching.com Calculer La Surface D Un Cercle - Maelynn.fr
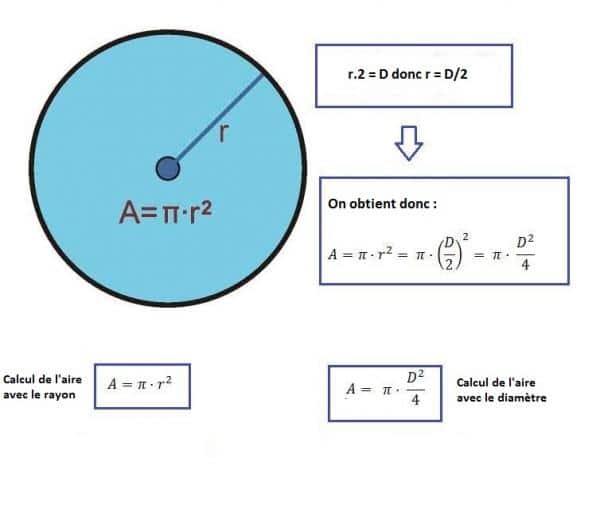www.maelynn.fr cercle calculer calcul perimetre maelynn crédits uccdn
Différence Entre Un Cercle Et Une Sphère
jeretiens.net Cercle trigonométrie formules cosinus et le les la pi maths cos sin sinus tangente tan calcul math circle choose board. Cercles formules polygones feuille. 3. faire des cercles
Aucun commentaire:
Enregistrer un commentaire